Hier kannst du kostenlos und interaktiv das Mathe Grundschul-Thema Mathe Klasse 2 im Dezember lernen.
Lerne jetzt mit der beliebten Lernanwendung Schlaukopf!
Zusätzlich erhältst du im Folgenden eine Schritt für Schritt Anleitung wie du dich optimal auf einen Mathematik Test zu diesem Thema in der 2. Klasse vorbereiten kannst.
1. Schritt: Was muss ich wissen?
Verschaffe dir zuerst einen Überblick darüber, was du zum Thema Mathe Klasse 2 (im Dezember) wissen musst.
1.1 Zehner und Einer (Stellentafel)
In der zweiten Klasse haben die Kinder die Zahlen bis 20 kennengelernt. Im Zahlenraum bis 100 gibt es nun viele zweistellige Zahlen. Es ist nun wichtig die Zehnerstelle von der Einerstelle unterscheiden zu lernen. Bei einer zweistelligen Zahl stehen die Zehner immer an erster Stelle und die Einer stehen an der zweiten Stelle. Dies lässt sich anhand einer Stellentafel verdeutlichen. Die Zehner werden dort an erster Stelle eingetragen die Einer an der zweiten Stelle. Die Zahl 54 beispielsweise hat somit 5 Zehner und 4 Einer.
Die Sprechweise im deutschen ist allerdings umgekehrt: Man nennt zuerst die Einer und dann die Zehner (zum Beispiel vier-und-fünfzig). Es ist wichtig diesen Unterschied zur Schreibweise zu kennen. Dabei kann die Stellentafel ein wichtiges Hilfsmittel sein. Auch wenn es später darum geht zweistellige Zahlen miteinander zu addieren oder subtrahieren muss der Unterschied zwischen Zehner- und Einerstelle klar sein.
Die Stellentafel
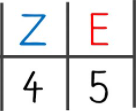
Mit einer Stellentafel kannst du den Wert der jeweiligen Ziffer einer Zahl ablesen. In diesem Fall geht es nur um die Zehner und die Einerstelle. Später werden auch die Hunderter- Tausender- oder Zehntausenderstelle dazukommen. Die Zehnerstelle wird mit einem Z abgekürzt. Die Einerstelle mit einem E. Möchtest du eine Zahl in die Stellentafel eintragen so überlege dir zuerst, welche stelle die Zehner und welches die Einerstelle ist und trage sie dann ein.
Beispiel:
Trage die Zahl 45 in die Stellentafel ein.
Die 45 besteht aus 40 und 5.
1.2 Addieren zum Nachbarzehner
Die Kinder lernen in der Grundschule im Dezimalsystem zu rechnen. Dies bedeutet alle Rechenoperationen werden auf die Zahl 10 bezogen. In der ersten Klasse haben die Kinder die Zahlen bis 20 kennengelernt. Sie haben gelernt Zahlen ohne Zehnerübergang miteinander zu addieren oder subtrahieren. Nun ist es im nächsten Schritt wichtig auch das Rechnen über den Zehner hinaus zu erlernen.
Das Rechnen mit Zehnerübergang erfolgt am besten in Schritten. Zuerst müssen die Kinder lernen die Einerstelle bis zum nächsten Zehner aufzufüllen. Das bedeutet zur Zahl der Einerstelle so viel dazuzuzählen, dass man die Zahl 10 erhält. Das bedeutet bei einer zweistelligen Zahl wird zur Einerstelle so viel dazugezählt bis sich die Zahl 10 ergibt. Dadurch gelangt man zum nächsten Zehner. Von dieser Zahl aus muss man dann noch die verbleibende Menge oder Zahl zur Zehnerzahl addieren. Zusammenfassend bedeutet dies, dass die Kinder zuerst lernen müssen wie man zum nächsten Zehner rechnet und von dort aus, die noch verbleibende Zahl zur Zehnerzahl hinzuzählt. Der erste Schritt bezieht sich dabei nur auf das Addieren, das heißt dass hinzuzählen der Einer zur letzten Stelle der zweistelligen Zahl.
Du hast schon gelernt wie man zwei Zahlen zusammenzählt. Nun geht es darum die Zahl zu finden die bis zum nächsten Nachbarzehner fehlt. Das heißt: Welche Zahl muss zu deiner Zahl addiert werden um zum nächsten Nachbarzehner zu gelangen?
Beispiel:
23 + 7 = 30 Es müssen sieben addiert werden.
45 + 5 = 50 Es müssen fünf addiert werden.
Merke: Um zum nächsten Nachbarzehner zu gelangen musst du immer eine einstellige Zahl addieren.
1.3 Zahlenreihen
Zahlenreihen werden auch als Zahlenfolgen bezeichnet. Beim Thema Zahlenreihen geht es darum Muster und Prinzipien zu erkennen. Sie kommen in der Grundschule entweder als normale Zahlenreihen oder als Zahlenschlangen vor. Sie folgen immer demselben Prinzip. Man muss das Muster hinter der Zahlenreihe erkennen um die Zahlenreihe dann selbst fortführen zu können. Es ist möglich, dass man zur Bildung einer Zahlenreihe immer nur dieselbe Zahl zur letzten Zahl addieren oder subtrahieren muss. Es gibt aber auch Zahlenreihen die komplizierter sind. Zum Beispiel ist es auch möglich, dass man zuerst eine bestimmte Zahl addieren und danach eine andere Zahl subtrahieren muss. Dieser Schritt wird dann immer wiederholt. Dadurch ergibt sich eine bestimmte Reihe von Zahlen. Die Aufgabe der Schüler ist es nun herauszufinden, welche Zahl man addieren oder subtrahieren (bzw. multiplizieren oder dividieren muss) um die Zahlenreihe zu erhalten.
Jede Zahlenreihe gehorcht also einem bestimmten Bildungsgesetz. Dieses Bildungsgesetz zu erkennen und selbst die Zahlenreihe fortführen zu können ist der Sinn dieser Übungen. Am besten geht man dabei Schritt für Schritt vor. Man schaut sich zuerst die erste Zahl an und überlegt wie man zur zweiten Zahl gelangen könnte. So macht man es dann auch mit der zweiten und der dritten Zahl und so weiter. Es macht Sinn die einzelnen Schritte über den Zahlen zu notieren. Hat man die Regel für die Bildung der Zahlenreihe erkannt, so kann man die Zahlenreihe selbst fortführen.
Der Name sagt es bereits. Bei Zahlenreihen handelt es sich um eine Aneinanderreihung von Zahlen. Am Ende der Folge – oder auch zwischendrin – fehlt eine Zahl, die du ergänzen musst. Die Zahlen sind aber nicht einfach wahllos aneinandergereiht, sondern nach einer bestimmten Regel. Du musst diese Regel erkennen, um die Reihe sinnvoll zu vervollständigen.
Momentan musst du zum Lösen der Zahlenreihen entweder eine Zahl addieren oder subtrahieren. Später kommen noch das Multiplizieren und Dividieren hinzu.
Merke: Bei Zahlenreihen geht es darum die Regel der Zahlenfolge zu erkennen und dann die richtige Lösung daraus abzuleiten.
Beispiel:
2, 4, 6, 8 (immer +2)
2, 4, 9, 11, 16 (immer zuerst +2 dann +5)
20, 15, 17, 12, 14 (immer zuerst -5 dann +2)
Da die Themen nicht von allen Klassen immer in derselben Reihenfolge behandelt werden, solltest du auf jeden Fall auch in deinem Heft nachschauen, welche Themen ihr behandelt habt.
Du solltest diesen Lernstoff gut üben. Am besten du schaust zusätzlich in dein Heft oder deinen Order.
2. Schritt: Sich abfragen lassen
Um das gelernte Wissen zu vertiefen ist es am besten, wenn du dich das Thema abfragen lässt. Auf der Seite schlaukopf.de kannst du interaktive Fragen zum Thema Mathe Klasse 2 (im Dezember) beantworten und dein Wissen testen.
https://www.schlaukopf.de/grundschule/klasse2/mathematik/monat/dezember
Du kannst das Gelernte auch deinen Mitschülern oder Eltern erklären. Dabei lernst du auch komplizierte Zusammenhänge besser zu verstehen.
3. Schritt: Mit Tests oder Übungsblättern lernen
Eine tolle Möglichkeit dich auf einen Test vorzubereiten, wenn du dich schon ein bisschen in das Thema eingearbeitet hast, ist das Bearbeiten von Tests, Klassenarbeiten oder Übungsblättern.
Du lernst dabei auch gleich die Fragestellungen kennen und bekommst ein Gefühl dafür, worauf es beim Lernen des Themas ankommt.
Hier findest du garantiert eine Menge guter Klassenarbeiten und Übungsblätter:
https://www.klassenarbeiten.de/grundschule/klasse2/mathematik/

Am besten druckst du dir die Tests mit Lösung aus. Dann kannst du sogar die richtige Klassenarbeits-Situation nachstellen. Behalte auch die Zeit im Auge. Wie schnell bist du im Bearbeiten der Aufgaben?
4. Schritt: Schaue dir ein Lernvideo an
Hast du das Thema gut gelernt, dich abfragen lassen und ein paar Tests oder Übungsblätter durchgearbeitet, so kannst du dich jetzt zurücklehnen und dir ein Lernvideo zum Thema anschauen.
Dadurch behältst du den Überblick und bekommst nochmal einen Überblick über das ganze Thema.
Wenn du in die Suchmaschine zum Beispiel folgende Begriffe eingibst, findest du Videos zum Thema:
"Zahlenreihen Video"
"Stellentafel Video"
"Ergänzen zum Zehner Video"
Hast du alle diese Punkte beachtet, dann bist du jetzt super vorbereitet. Dein Test kann kommen!
5. Lernziele
Das solltest du nach dem Lernen können:
- Wissen was eine Stellentafel ist und Zahlen in die Stellentafel eintragen können.
- Zehner und Einer einer Zahl bestimmen können.
- Zahlenreihen verstehen und fortsetzen können.
- Eine Zahl zum nächsten Zehner ergänzen können.